Priority Queue
우선순위가 가장 높은 값이 먼저 추출되는 자료구조
1. 리스트 방식
•
dequeue를 위해서는 전체를 탐색하기 때문에 n번의 연산이 필요하다.
시간복잡도
•
enqueue() :
•
dequeue() :
2. 정렬 방식
•
queue에 데이터를 넣고나서 정렬을 해주는 방법. 정렬은 의 시간 복잡도를 가진다. 따라서 데이터를 넣을 때마다 정렬을 해주므로 . 정렬 이후에는 앞에서 빼든 뒤에서 빼든 한번의 연산이 필요하다.
시간복잡도
•
enqueue() :
•
dequeue() :
3. 완전이진트리
•
가장 낮은 숫자를 위로 올린다. 1번 노드가 추가가 되면 가장 작은 숫자이기 때문에 우선순위가 높다. 그래서 가장 Top의 노드와 순서를 바꾼다.
enqueue도 입력된 이후, 가장 작거나 높은 숫자를 위로 올려야 한다. 반대로 dequeue된 후에도 가장 높은 숫자를 위로 올려야하기 때문에, 둘 다 그래프의 높이인 의 시간복잡도를 가진다.
시간복잡도
•
enqueue() :
•
dequeue() :
구현 1, 2, 3비교
•
enqueue, dequeue가 둘 다 으로 가능하기 때문에 전체적으로 시간복잡도가 낮다고 생각할 수 있다. 따라서 완전이진트리를 사용해 구현을 할 것인데, Heap이라는 자료구조를 사용할 것이다.
, 보다 이 훨씬 작다.
Priority Queue를 위한 자료구조 Heap
완전 이진 트리의 자료구조이다. Heap 자료구조가 완전 이진 트리 그 자체이다. Heap만 구현한다면, Priority Queue 그 자체가 된다.
완전 이진 트리를 리스트로 구현하면, 생각보다 간단해진다.
•
min heap: 부모 노드의 값이 자식 노드의 값보다 작은 트리 형태의 자료구조
•
max heap: 부모 노드의 값이 자식 노드의 값보다 큰 트리 형태의 자료구조
형제 노드 간에는 대소 관계가 정해지지 않는다. Root 노드가 가장 큰(or 작은) 값을 가진다.
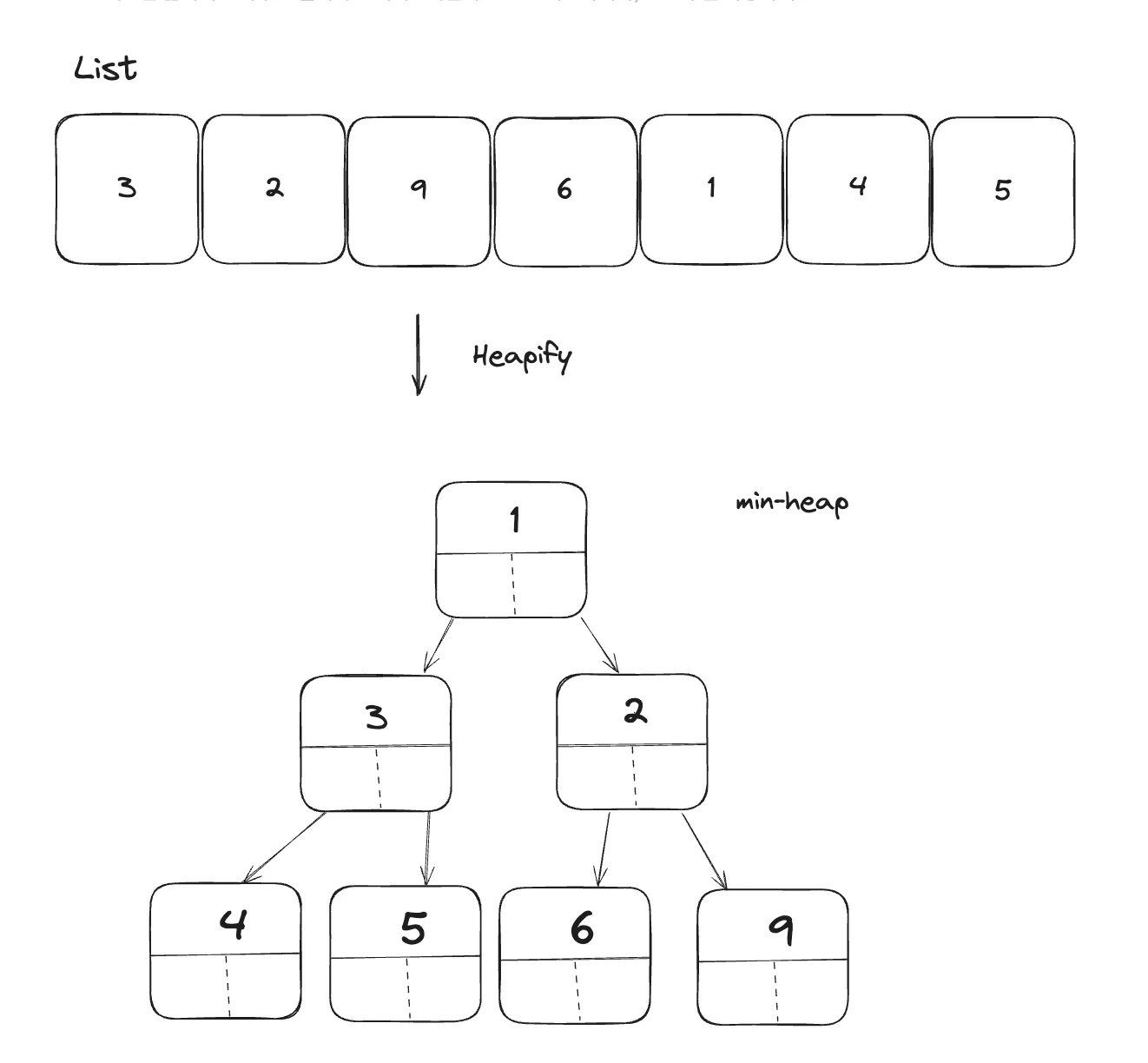
Heapify
리스트를 Heap 자료구조화 하는 과정
시간복잡도
•
Heappop
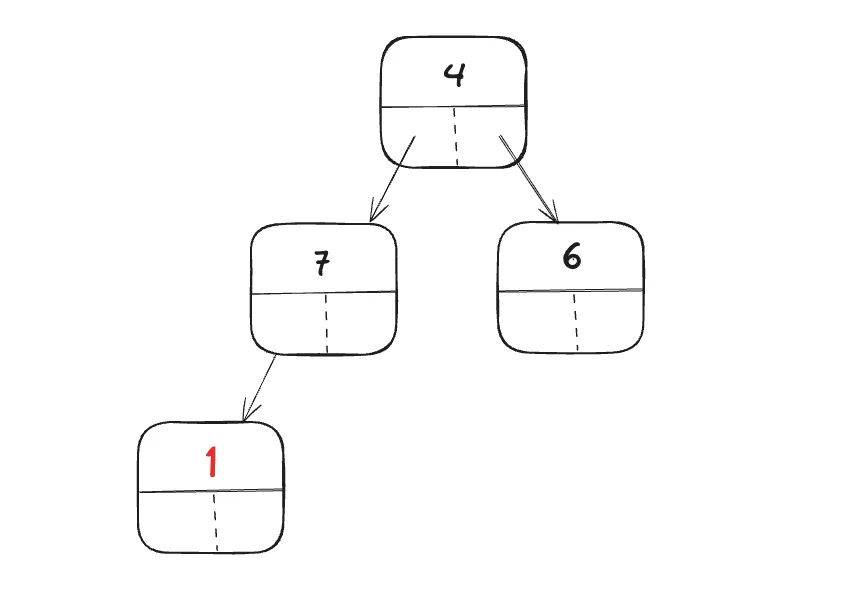
1.
pop이 되고나서 맨 마지막 노드를 Root로 보낸다.
2.
우선순위가 높은 자식 노드랑 스위치한다.(sift-down) 아무리 많이 연산을 해도 logn만큼이다.
min-heap에서 숫자가 작은 노드가 우선순위가 높고, max-heap에서는 숫자가 큰 노드가 우선순위가 높다.
시간복잡도
•
Heappush
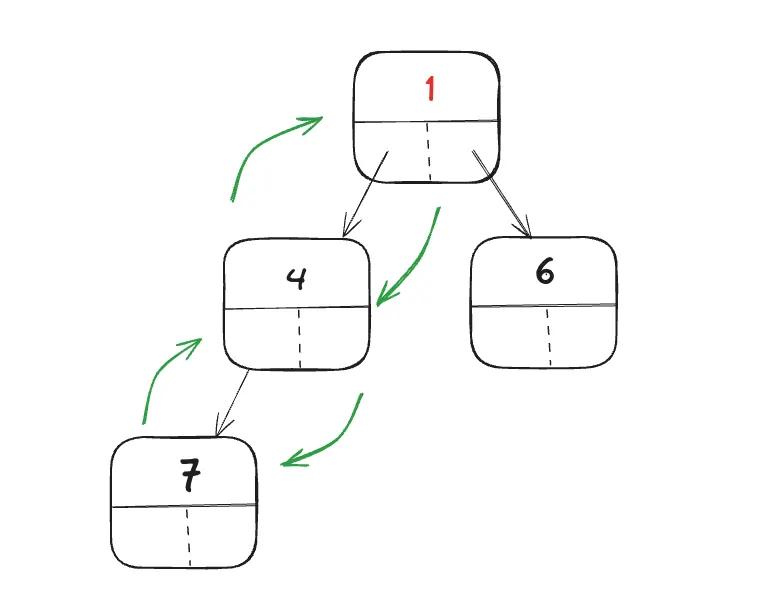
1.
맨 마지막 노드에 추가를 해준다.
2.
우선순위가 낮은 부모 노드랑 스위치한다.(sift-up) 아무리 많이 연산을 해도 만큼이다.
 코드
코드
import heapq
min_heap = [3, 2, 9, 6, 1, 4, 5]
heapq.heapify(min_heap)
heapq.heappop(min_heap)
heapq.heappush(min_heap, 1)
max_heap = [3, 2, 9, 6, 1, 4, 5]
heapq._heapify_max(max_heap)
value = heapq._heappop_max(max_heap)
# min-heap을 이용한 max-heap 구현
max_heap = [i * - 1 for i in max_heap]
heapq.heapify(max_heap)
weight = heapq.heappop(max_heap)
value = -1 * weigth
Python
복사